Minitabda Kontrol Grafikleri Nasıl Çizilir?
Minitabda Kontrol Grafikleri, Bu yazımızda sizlerle Minitab da formüllere girmeden kontrol grafiklerinin nasıl çizildiğini göstereceğiz.
Bir çok kişi kontrol grafiklerinin çizimini ve takibini Excel üzerinden yapmakta; fakat excelde formüllere müdahale edilebilmesi sonucun değişmesine ve sizinde yanlış bilgi ile yanlış karar vermenize sebep olabilir. Bu tür hatalara kuruluşlara gittiğimizde görmekteyiz. Sadece İPK için değil diğer istatistiksel tekniklerde de bu tarz sıkıntılar yaşanmakta.
Bu tarz sıkıntıları yaşamamak için Minitab gibi istatistiksel programları tercih etmemizde fayda var ki artık birçok büyük kuruluş tedarikçilerinden Minitab vb. programları kullanmaları için istekte bulunuyor.
Şimdi gelin Minitab’ da kontrol grafiklerini beraber çizelim.
Hangi Kontrol Grafiğini Çizeceğim?
İlk yapmamız gereken hangi kontrol grafiğini çizeceğimize karar vermek. Hangi kontrol grafiğini çizeceğimize de veri tipine bakarak karar vereceğiz.
Prosesinizden topladığını veriler eğer uzunluk, ağırlık, sıcaklık, basınç, vb… gibi ölçülebilir veriler ise (sürekli veri) I-MR, XBar-R veya Xbar-S kontrol grafiklerini çizebiliriz. Örnek verecek olursak CNC den çıkmış bir parçanın dış çap uzunluğu, bir fırının sıcaklığı, bir ipin mukavemeti, bir ürünün ağırlığı, vb…
Diğer taraftan verileriniz birim başına düşen hata sayısı veya geçer geçmez, geçti kaldı gibi 2 sonucu olan veriler ise (kesikli veri) bu verilerle de p veya u grafiklerini çizebiliriz. Örnek verecek olursak; final kontrolde bir gömlek üzerindeki hata sayısı, bir operatörün bir parçayı geçti kaldı diye ayırması, vb…
Öncelikle sürekli veriler için olan I-MR (X-MR) ve Xbar-R grafiklerini çizelim.
I-MR (X-MR) Kontrol Grafiği Nasıl Çizilir?
I-MR; Individual Moving Range ingilizce kelimelerin baş harflerinden oluşur. Bazı kaynaklarda Individual yerine her bir veriyi temsil eden X’ leri kullanarak X-MR şeklinde de görebilirsiniz. Bu tür bir grafiği çizebilmeniz için veri türünüzün ölçülebilir yani sürekli veri olması gerekmektedir.
Bu grafiği çizebilmemiz için prosesiniz de bir defada bir adet ürün için (alt grup örnek sayısı=1) elde ettiğiniz ölçüm değerine göre oluşturulur. Biraz daha açacak olursak prosesinizden bir defada bir ürün çekiyor ve bunun bir karakteristiğini ölçüyorsanız bu grafik türünden yararlanabilirsiniz.
Örnek bir uygulama üzerinden giderek I-MR Grafiğini beraber çizelim.
I-MR Örnek: Aşağıdaki laboratuvar sonuçları, süt tozu nem yüzdelerini göstermektedir. Analiz edilen süt tozuna ait her bir örnek, bir lotu temsil eder. Tek bir lot içindeki varyasyon anlam taşımayacağından her bir lottan bir örnek alınmasına karar verilir.
Bu prosesi kontrol altında tutmak gerekmektedir.
| Lot | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Nem % | 2.9 | 3.2 | 3.6 | 4.3 | 3.8 | 3.5 | 3 | 3.1 | 3.6 | 3.5 |
Örnekte de görüldüğü gibi her defasında bir adet verimiz bulunmakta.
Minitab’ da takipteki patikayı kullanarak Resim-1 deki menüye ulaşırız. Resim-1 de ki menüde ayrıca I-MR Options’ ı tıklayarak Tests Sekmesinde Tüm testlerin yapılmasını işaretleriniz (Resim-2)
I-MR Kontrol Grafiği için Minitab Patikası:
Stat > Control Charts > Variables Charts for Individuals > I-MR
Resim-1: I-MR Chart
Resim-2: I-MR Chart Options
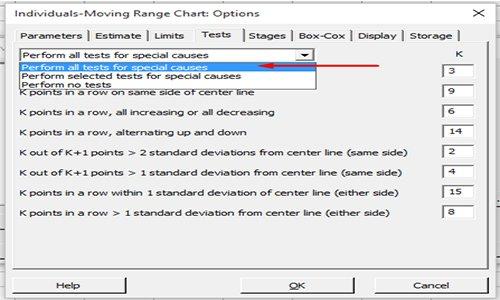
Resim-1 deki I-MR menüsünde OK bastığımız zaman takipteki I-MR grafiğini elde ederiz (Grafik-1)

I-MR grafiği içerisinde 2 grafik görmekteyiz. Bunlardan I (Individuals) grafiği üst tarafta ve her bir veri zamana bağlı olarak çizilmiş.
Alttaki grafik ise ardışık verilerin farklarından elde edilen verilerle çizilmiş MR (Moving Range) grafiği (dikkat ettiyseniz ardışık sayıların farkları alındığı için 2. veriden çizilmeye başlanmış).
MR grafiği bize veriler arasındaki farkın zamana bağlı değişimini yani yayılmayı göstermekte. MR grafiğinde kontrol limitlerini aşmadığını ve tüm testlerden geçtiğini görmekteyiz.
Üstteki I grafiği ise her bir verinin zamana bağlı değişimini yani yığılmayı göstermekte. Bu grafiğinde kontrol limitlerini aşmadığını ve tüm testlerden geçtiğini görmekteyiz.
Xbar-R Kontrol Grafiği Nasıl Çizilir?
Xbar-R; kontrol grafiği ortalama ve aralık değerlerinden elde edilen 2 grafikten oluşur.
Bu tür bir grafiği çizebilmeniz için veri türünüzün ölçülebilir yani sürekli veri olması gerekmektedir.
Bu kontrol grafiğinde I-MR dan farklı olarak her defasından çekilen örneklemde alt grup örnek sayısı 2 ile 9 arasında bir sayı olması gerekmektedir. Biraz açacak olursak prosesimize gidip her defasında 3 adet örnek alırsak (alt grup örnek sayısı) bu örnekler ile Xbar-R grafiğini çizebiliriz.
Burada alt grup örnek sayısı 8 veya 9 u geçer ise Xbar-S grafiğinden yararlanabiliriz.
Örnek bir uygulama üzerinden giderek Xbar-R Grafiğini beraber çizelim.
Örnek-2: Aşağıdaki tabloda, buji dış yarıçapına ait değerler verilmiştir. Bu değerler, 20 alt grup olarak, her yarım saate bir alınmıştır. Her alt grupta 4 örnek vardır (alt grup örnek sayısı=4). Her satır bir örneklemi göstermektedir.
| Alt Group No. | Yarıçap | |||
|---|---|---|---|---|
| x₁ | x₂ | x₃ | x₄ | |
| 1 | 0.1898 | 0.1729 | 0.2067 | 0.1898 |
| 2 | 0.2012 | 0.1913 | 0.1878 | 0.1921 |
| 3 | 0.2217 | 0.2192 | 0.2078 | 0.198 |
| 4 | 0.1832 | 0.1812 | 0.1963 | 0.18 |
| 5 | 0.1692 | 0.2263 | 0.2066 | 0.2091 |
| 6 | 0.1621 | 0.1832 | 0.1914 | 0.1783 |
| 7 | 0.2001 | 0.1927 | 0.2169 | 0.2082 |
| 8 | 0.2401 | 0.1825 | 0.191 | 0.2264 |
| 9 | 0.1996 | 0.198 | 0.2076 | 0.2023 |
| 10 | 0.1783 | 0.1715 | 0.1829 | 0.1961 |
| 11 | 0.2166 | 0.1748 | 0.196 | 0.1923 |
| 12 | 0.1924 | 0.1984 | 0.2377 | 0.2003 |
| 13 | 0.1768 | 0.1986 | 0.2241 | 0.2022 |
| 14 | 0.1923 | 0.1876 | 0.1903 | 0.1986 |
| 15 | 0.1924 | 0.1996 | 0.212 | 0.216 |
| 16 | 0.172 | 0.194 | 0.2116 | 0.232 |
| 17 | 0.1824 | 0.179 | 0.1876 | 0.1821 |
| 18 | 0.1812 | 0.1585 | 0.1699 | 0.168 |
| 19 | 0.17 | 0.1567 | 0.1694 | 0.1702 |
| 20 | 0.1698 | 0.1664 | 0.17 | 0.16 |
Xbar-R Kontrol Grafiği için Minitab Patikası:
Stat > Control Charts > Variables Charts for Subgroup > Xbar-R
Resim-3: Xbar-R Chart
Resim-4: Xbar-R Chart Options
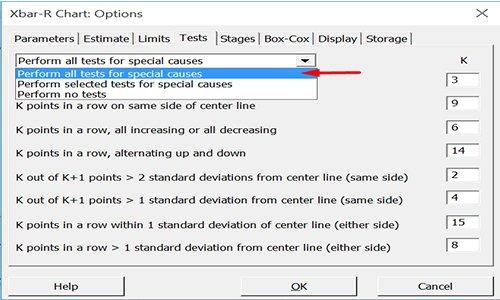
Resim-3 deki Xbar-R menüsünde OK bastığımız zaman takipteki Xbar-R grafiğini elde ederiz (Grafik-2)
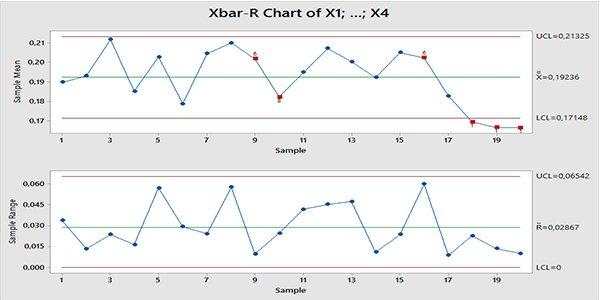
Xbar-R grafiği içerisinde 2 grafik görmekteyiz. Bunlardan “Xbar” grafiği üst tarafta ve her bir alt grubun ortalaması alınarak zamana bağlı olarak çizilmiş.
Alttaki grafik ise her bir alt grubun en büyük ve en küçük değerleri arasında fark alınarak elde edilen verilerle çizilmiş “R” (Sample Range) grafiğidir.
“R” grafiği (sample range) bize her bir örneğin kendi içindeki range değerlerinin zamana bağlı değişimini yani yayılmanın zamana bağlı değişimini göstermekte. “R” grafiğinde kontrol limitlerini aşmadığını ve tüm testlerden geçtiğini görmekteyiz.
Üstteki “Xbar” (Sample Mean) grafiği ise her bir örneklemin ortalamasının zamana bağlı değişimini yani yığılmanın zamana bağlı değişimini göstermekte. Bu grafiğinde son 3 örneklem ortalamasının kontrol limitlerini aştığını görmekteyiz. Burada aynı zamanda test 6 dan da geçmediğini görmekteyiz.
Şuan proses de özel nedenlerin devreye girdiğini görmekteyiz. İlk yapılması gereken kontrol limitlerini aşan değerleri yani bu grafikteki son 3 örneklemi atarak tekrar kontrol grafiklerini çizmek olacak.
Yeni çizeceğimiz kontrol grafiği eğer tüm testlerden geçerse artık o kontrol grafiğindeki kontrol limitlerini kullanabiliriz.



